Der katalanische Philosoph und Theologe Raimundus Lullus (1232-1315) entwickelte in seinem Werk ›Ars magna‹ ein revolutionäres System mit dem Ziel, Ungläubige zum Christentum zu bekehren. Diese in mehreren Versionen erschienene Kunst (›Ars generalis ultima‹, ›Ars inventiva‹, ›Ars demonstrativa‹) basiert einerseits auf den Lehren der griechischen Philosophen Aristoteles und Platon, andererseits auf arabischen sowie jüdischen Einflüssen.

Dieses epochale Werk durchläuft innerhalb von dreißig Jahren zwei Entwicklungsstufen, wobei die Absicht einer Vereinfachung der durchaus komplizierten philosophischen Vorläufer deutlich wird. Alle Ausgaben der ›Ars‹ bestehen aus einem Textteil sowie einem Bildteil, in dem verschiedene diagrammartige Figuren zu sehen sind. 1308 entsteht die ›Ars brevis‹, die am weitesten verbreitete Version, in der durch Erklärungen bzw. Anleitungen zum Gebrauch der Figuren der Zugang zu den ausführlicheren Ausgaben erleichtert wird. Lullus verwendet eine Kombinatorik (Künzel 1986: 159 ff.) allgemeiner Prinzipien, die von den drei großen monotheistischen Religionen akzeptiert werden und versucht damit, die konfliktträchtige Tradition der Textinterpretation der jeweiligen heiligen Schriften (Bibel, Talmud, Koran) zu durchbrechen. Mit Hilfe der in der ›Ars‹ vorgegebenen Begriffe und den dargestellten Figuren kann der Leser verschiedene Kombinationen nutzen, um Sätze zu bilden. Diese Sätze fungieren als Grundgerüst, um eine universelle Wahrheit zu finden und letztendlich sein Gegenüber in einer Diskussion argumentativ vom christlichen Glauben zu überzeugen.

Einige Missionsreisen führten den Gelehrten nach Nordafrika, jedoch verlief seine letzte Reise nicht erfolgreich. 1314 sollte er von einer aufgebrachten Menschenmenge in Algerien gesteinigt werden. Lullus überlebte zwar, verstarb allerdings ein Jahr später auf Mallorca.

Lullus‘ Schriften wurden 1376 durch den Papst verboten und von der Inquisition bis 1416 eingezogen, so dass sie zunächst nur im Verborgenen studiert werden konnten. Nikolaus von Kues, einer der ersten deutschen Humanisten, gilt als heimlicher Anhänger des Lullismus. In der Renaissance und im Barock rezipierten die Gelehrten Lullus‘ Vermächtnis wieder öffentlich. Im 19. Jahrhundert wurde der nun als Märtyrer anerkannte Lullus von Papst Pius IX. selig gesprochen.

Erst seit der Mitte des 20. Jahrhunderts wird Raimundus Lullus‘ Einfluss auf die Wissenschaften erforscht. In unserem Beispiel ist seine bahnbrechende Erfindung zu sehen: Ein Vorläufer unserer heutigen Computer.

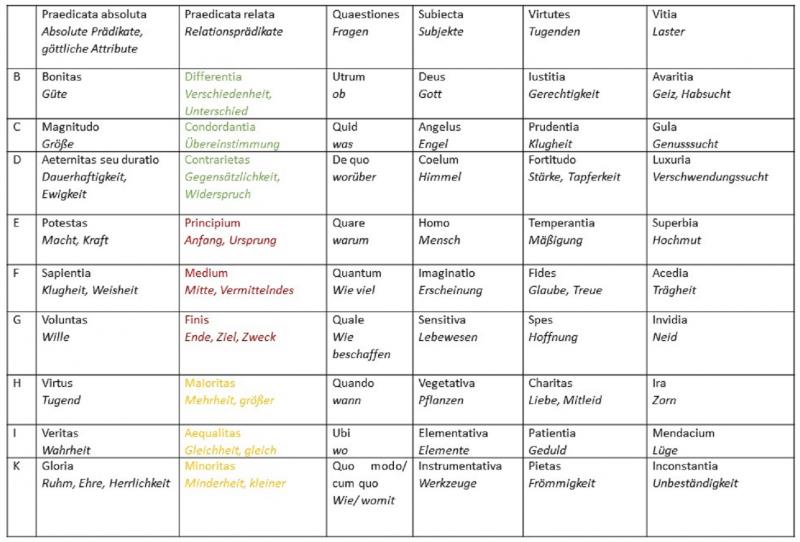
Figur A: die neun grundlegenden Prinzipien der ›Ars‹. Sie sind alle untereinander kombinierbar und können, wenn sie vereint sind, als Gottesbeweis verstanden werden. Der Buchstabe ›A‹ steht für den Schöpfer und wird nur in dieser Figur verwendet. ›A‹ ist der erste Buchstabe des phönizischen und hebräischen Alphabets (Aleph = א), er hat den Zahlenwert 1. Die jüdische Aleph-Theorie interpretiert diesen Buchstaben als Hauch Gottes bzw. als Offenbarung.

Figur T: drei versetzt übereinander gelegte Dreiecke, die innerhalb eines Kreises angeordnet sind. Sie enthält die relativen Prinzipien, denen jeweils Buchstaben zugeordnet werden.

Figur 3: Tabelle in Form eines Dreiecks mit allen möglichen Zweierkombinationen ohne Wiederholung der ersten beiden Figuren.

Figur 4: dreiteilige Drehscheibe, auf jeder Scheibe stehen die neun Buchstaben. Diese rotationsfähige Kombinationshilfe generiert mechanisch alle Dreierkombination (siehe Video).

In der Handschrift 1895/1428 4° aus der Trierer Stadtbibliothek findet sich eine Abbildung von vier Figuren der ›Ars‹. Diese Ausgabe beginnt mit der ›Ars brevis‹ als Einführung und enthält danach die ›Ars inventiva‹ sowie die ›Ars demonstrativa‹. Die von Raimundus Lullus entwickelte Kombinatorik beruht auf der Idee einer logischen Berechnung und deren Automatisierung. Um sinnlose Kombinationen auszuschließen, verwendet Lullus einen Algorithmus, so dass die Drehscheiben nur sinnvolle Verknüpfungen anzeigen. Diese Prinzipien gelten auch für die moderne Informationstechnologie.

Das System beruht auf vier zentralen Figuren und auf dem ›Alphabet des menschlichen Denkens‹ (siehe Abb.2). Mit den Begriffen dieses Alphabets werden die Figuren gefüllt, so dass jeder Buchstabe verschiedene Bedeutungen tragen kann. Die Kombination ›BC‹ kann beispielsweise als Grundlage für etwa 50 Aussagen und Fragen dienen. (Güte ist groß; Größe ist einheitlich; Welcher Unterschied ist groß?; Welche Güte ist groß?; Was ist die unterschiedene Güte? usw.) Insgesamt bietet die ›Ars‹ 9³ = 729 Wahlmöglichkeiten, verteilt auf vier Figuren.

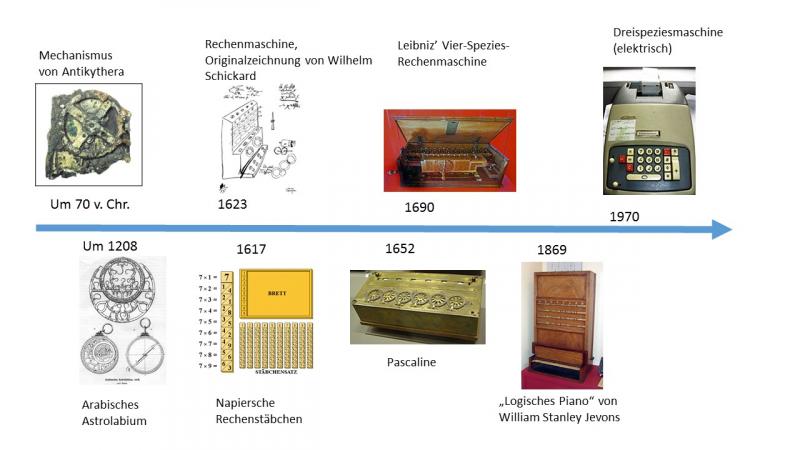
Schon um 250 v. Chr. entstanden sog. ›Astrolabien‹, scheibenförmige Geräte, die für astronomische Berechnungen, als Zeitmesser sowie als Kalender genutzt wurden. Die Funktionsweise des ›Mechanismus von Antikythera‹, eines hochkomplexen antiken Instruments, konnte erst nach Jahrzehnten entschlüsselt werden. Dieses Gerät diente zur Bestimmung der Positionen von Himmelskörpern, es konnte sogar zur Berechnung einer Sonnenfinsternis eingesetzt werden. Heute gilt es als erster Computer der Welt (vgl. Price 1975).

Doch das Wissen des Altertums ging verloren. In den Jahrhunderten nach dem Ende der Antike blieben mechanische Geräte auf Uhrenmechanismen und einfache Astrolabien beschränkt. Im 17. Jahrhundert entstanden die ersten Rechenmaschinen mit einem Addier- und Subtrahierwerk. Das Multiplizieren wurde mit den seit 1617 bekannten ›Napierschen Rechenstäbchen‹ vorgenommen. Der Einfluss der Schriften von Raimundus Lullus auf die Erfinder der Maschinen ist spätestens bei Gottfried Wilhelm Leibniz offensichtlich: Seine Ideen der Logik, Kombinatorik und des Algorithmus werden quasi vom Pergament auf das Räderwerk der Apparate übertragen.

1666 rezipierte Leibniz die ›Ars magna‹ in seinem Werk ›Dissertatio de arte combinatoria‹, wobei er auch Lullus' ›Alphabet‹ übernimmt. »Die Ars Magna des Raimundus Lullus hat noch einigen Bezug zu dem, was ich vorschlage. Denn man nimmt seinen Ausgang bei einigen allgemeinen Begriffen, wie Magnitudo, Potentia, Duratio, Virtus, welche man auf alle Arten von Dingen anwenden kann, und das gibt einem die Mittel, durch ihre Kombination weitreichende Erörterungen über beliebige Gegenstände anzustellen« (Leibniz 1679). Das Prinzip einer Automatisierung durch das Kombinieren von Buchstaben verband Leibniz mit seiner ›mathesis universalis‹, einer generalisierten Mathematik. Einige Jahre später stellte er die erste Konstruktion seiner Rechenmaschine in London vor.

Auch Lullus' Ansatz der Begriffslogik wurde weiterentwickelt, als Beispiel wäre das ›Logische Piano‹, ein mechanisches Gerät zur Bildung von Begriffskombinationen von 1869 zu nennen. Es sollte allerdings noch ein Jahrhundert vergehen, bis die Entwicklung dieser Maschinen durch die Entdeckung der Elektrizität vorangetrieben wurde. Dieser Prozess gipfelte in der Erfindung des Computers, wie wir ihn heute kennen.